|
|
► 9. ¿Y si...? Curiosidad, intuición y conjeturas
► 9.3 Segmentos
Objetivos
El razonamiento inductivo es una gran ayuda para establecer rápidamente conjeturas que puedan conducirnos hacia la comprobación o demostración de resultados veraces. Sin embargo, debemos mostrar los riesgos que entrañan las inducciones basadas en pautas numéricas cuya regularidad no se acompañe de algún argumento razonable.
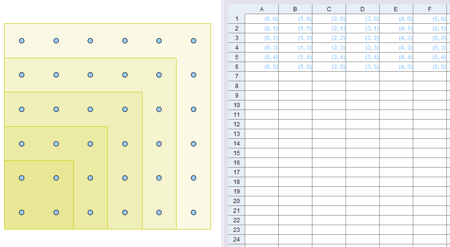
Aquí mostraremos un ejemplo, a partir de una actividad muy sencilla de construir con GeoGebra. Creamos un geoplano ortogonal 5x5 y nos preguntamos cuántos segmentos de diferente longitud podemos encontrar.
Herramientas y comandos
Usaremos la Hoja de Cálculo para crear rápidamente los pivotes del geoplano. Posteriormente, bastará usar la herramienta:
|
|
Segmento |
Propuesta de construcción
Primero prepararemos el escenario.
|
|
Dibujaremos el "tablero de juego", una cuadrícula limitada. Introducimos los cuatro primeros puntos.
|
|
Ahora usaremos el arrastre propio de las hojas de cálculo para crear rápidamente el resto de los puntos.
|
|
Una vez finalizada la construcción, personalizamos la barra de herramientas
dejando únicamente (además de la herramienta fundamental para elegir y mover)
las herramientas
![]() Segmento
y
Segmento
y
![]() Elimina.
Elimina.
Comentarios
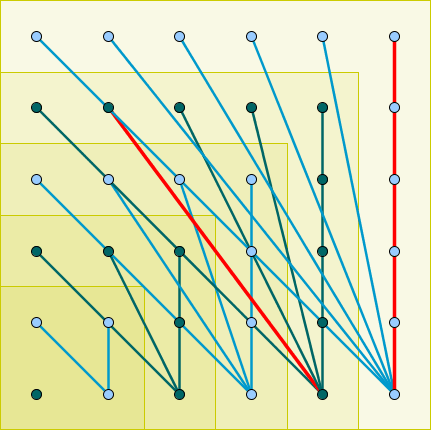
En la imagen anterior se puede observar que hemos añadido una lista de Polígonos para facilitar la visualización del proceso inductivo a medida que el geoplano va aumentando desde 2x2 hasta 5x5.
En el cuadrado inferior, 2x2, solo podemos trazar 2 segmentos de longitud diferente. En los siguientes cuadrados, uniremos el punto inferior derecho con los superiores obteniendo nuevos segmentos (los demás ya están contados). Así, obtenemos para cada geoplano la sucesión:
{2, 2 + 3, 2 + 3 + 4, 2 + 3 + 4 + 5, 2 + 3 + 4 + 5 + 6,...} = {2, 5, 9, 14, 20,...}
Parece, pues que se trata de una sucesión cuyas diferencias son {3, 4, 5, 6,...}. Incluso, observando que el producto de dos diferencias consecutivas [12, 20, 30...] es el doble del segundo término empleado más 2 unidades [2x5+2, 2x9+2, 2x14+2,...], podemos inferir que el término (n+1) será de la forma [(n+2)(n+3)-2]/2, o de forma equivalente, que el enésimo término es (n+3)n/2.
Sin embargo, no hemos tenido en cuenta que algunas diagonales pueden coincidir con tramos verticales u horizontales. En particular, resulta que los segmentos mostrados en rojo en la siguiente imagen tienen la misma longitud:
Así que en total no hay 20 segmentos de longitud diferente, sino solo 19. Este hecho desbarata nuestro patrón y la conjetura sobre el término general.
![]() Investigación:
Investigación:
- Trazar en GeoGebra una circunferencia y un número n (1, 2, 3...) de rectas secantes. ¿Cuál es el número máximo de trozos de círculo que podemos obtener? Experimentalmente, podemos obtener la serie {2, 4, 7, 11...} que parece apuntar a la término general (n-1)n/2 + 1. ¿Hay algún argumento lógico que podamos considerar para admitir este resultado o, por el contrario, puede que aparezca una "sorpresa" que desbarate esa pauta de crecimiento?