|
GeoGebra, el explorador matemático
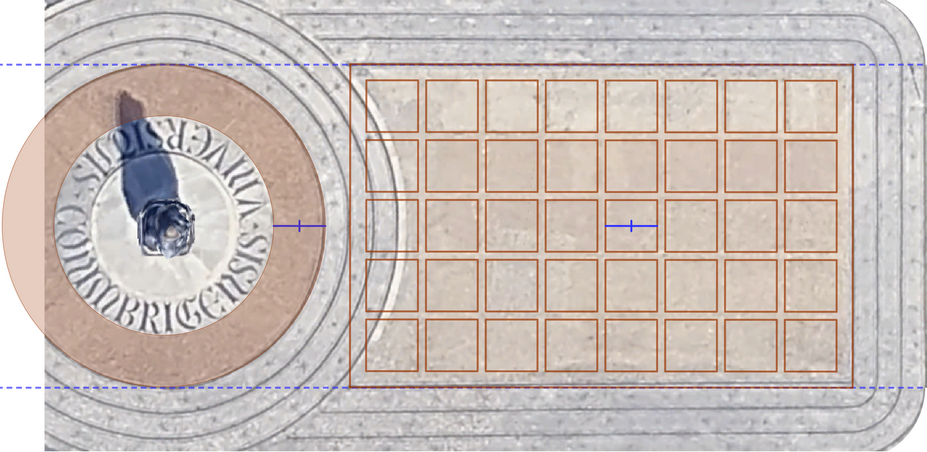
Vista cenital de la Estatua de Dom Dinis, con la inscripción UNIVERSITATIS COIMBRIGENSIS
rafael.losada@gmail.com II Congreso Internacional de GeoGebra Departamento de Matemáticas Facultad de Ciencias y Tecnología Universidad de Coímbra 23-25 octubre 2025
Rastro humano
La cabecera de esta página es una vista cenital de la estatua de Dom Dinis que se encuentra justo enfrente de este Departamento de Matemáticas de la Universidad de Coímbra. Como GeoGebra permite colocar imágenes como fondo de la vista gráfica, podemos resaltar los elementos que queramos y realizar indicaciones sobre ellos. Imágenes como esta son muy fáciles de obtener y permiten plantear un montón de preguntas según el nivel deseado, desde "¿Cuántos cuadrados aparecen?" o "¿Sabes calcular cuántos son sin contarlos uno a uno?", hasta "Tomando como unidad de superficie el área de cada cuadrado, ¿cuál es el área de la corona circular coloreada?" o "¿Cuál es el área de la parte visible del rectángulo (observa que los círculos que rodean a la estatua invaden parte de él?". Las herramientas de GeoGebra ayudan a los alumnos a explorar, calcular y comprobar sus conjeturas.
El legado de las Matemáticas es ubicuo. La siguiente imagen parece un cuadro abstracto, una pintura suprematista, pero en realidad es el rastro que el uso humano de las matemáticas ha dejado, en forma de parcelación agraria, a escasos 13 km al oeste de aquí, río abajo.
Google Maps @40.2036376,-8.5959846,1252m
Nos hallamos en la Universidad de Coimbra (UC), Patrimonio de la Humanidad desde 2013. Los nombres de algunas calles reflejan la profunda influencia de la Universidad en esta "ciudad de los estudiantes". A menos de 400 metros de aquí, podemos recorrer la Rua da Matemática, la Travessa da Matemática y el Largo da Matemática.
Desde hace más de un siglo, los estudiantes universitarios han fundado numerosas Repúblicas (comunidades de estudiantes, alrededor de 10 o 20, que comparten alojamiento, comidas, gastos, excursiones, fiestas y hasta bandera). En las imágenes, tres de estas repúblicas estudiantiles, situadas en los números 2, 6 y 40 de la Rua da Matemática (llamada así en honor a André do Avelar, que vivió allí).
Otros matemáticos históricos de la UC fueron Pedro Nunes, José Anastácio da Cunha, Miguel Franzini, Florêncio Mago Barreto Feio y Rodrigo Ribeiro de Sousa Pinto, que da nombre al barrio que está justo al lado de las Escadas Monumentais que bajan desde donde estamos:
El Día Internacional de las Matemáticas (Día de Pi, 14 de marzo) de este año 2025 estuvo dedicado a la creatividad común latente en el Arte y las Matemáticas. No debe extrañar, pues, que a lo largo de la historia el arte recurriera con frecuencia a las matemáticas en su búsqueda de métodos de construcción para representar la realidad, como el estudio de la perspectiva, o expresar la belleza, mediante propiedades como la proporcionalidad o la simetría.
No cuesta mucho encontrar ejemplos de esta relación a nuestro alrededor. A menos de 400 m de donde estamos se encuentra el claustro de la Sé Velha (siglo XIII), en el que podemos apreciar sus 20 rosetones, todos distintos (fotos de Mariló Fernández Mira, 2007). Cada una de las cuatro caras del claustro tiene cinco arcos ojivales, y cada uno de ellos abarca un rosetón y dos arcos de medio punto. En las esquinas, los arcos ojivales se intersecan a la altura de los arcos de medio punto, produciendo un curioso efecto.
He recolocado los rosetones sobre los mismos dos arcos de fondo, para mostrar sus diferencias y simetrías (obviando un ligero desperfecto que, curiosa o deliberadamente, aunque rompa la simetría rotacional, conserva la simetría diédrica). Estos rosetones tienen diseños sencillos, por lo que pueden ser propuestos para reconstruirlos con GeoGebra en enseñanza secundaria. Los 20 rosetones diedros tienen órdenes 3, 4, 5, 6 y 8, que corresponden a polígonos construibles, mientras que 7 no lo es (Ortega, Ortega, Ortega y Crespo, 2005). Este mismo claustro puede servir para proponer la construcción de arcos ojivales y de medio punto (Arranz, Losada, Mora y Sada, 2008 y 2009).
Seguramente la primera idea de uso del rastro activado sea la de dibujar, convertirlo en un lápiz. Por ejemplo, el uso del rastro con color facilita la creación y visualización de cualquier rosetón, ya sea cíclico o diedro (Losada, 2010).
Entremos ahora en el Museu Nacional Machado de Castro, a menos de 300 m de aquí.
En él se conservan catorce azulejos matemáticos del siglo XVIII que decoraban algunas aulas del antiguo colegio de los jesuitas. Tal como descubrió, en los años 90, António Leal Duarte (del Departamento de Matemáticas en el que nos encontramos), estos azulejos reproducen algunas figuras de una edición de los Elementos de Euclides (Tacquet, 1683), como aparece en la parte derecha de esta imagen (Requena, 2014).
Esta figura corresponde a la Proposición XVII del Libro III, en donde se dan y demuestran las instrucciones para trazar una tangente a una circunferencia por un punto de ella o exterior.
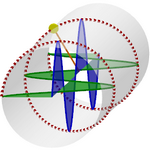
Antes de exponer más ejemplos del uso del rastro, recordemos que con GeoGebra resulta muy sencillo realizar inversiones en una circunferencia.
Aquí vemos cómo podemos crear fácilmente, por inversión en 2D, una cadena de Steiner, comprobando que la inversión mantiene las tangencias, pero los centros de los círculos ya no forman una circunferencia sino una elipse (verde).
Al pasarlo a 3D, la envolvente de las esferas que se invierten (en la esfera azul turquesa) forman un toro. La inversión de este toro en esa esfera, es decir, la envolvente de las correspondientes esferas invertidas, forman un cíclido de Dupin (en el caso de 6 esferas, el cíclido envuelve el sexteto de Soddy). Con infinitas esferas, obtenemos la cadena de Pappus, donde el cíclido de Dupin corresponde a la inversión de un cilindro.
Los azulejos geométricos más habituales no son azulejos matemáticos del tipo que hemos visto, sino aquellos pensados para repetir cierto patrón por teselación periódica. Aunque la influencia islámica de este tipo de arte es mayor en España que en Portugal, donde los azulejos más frecuentes tienen un carácter más figurativo que geométrico, no faltan ejemplos.
Podemos encontrar azulejos geométricos en la propia Sé Velha de Coimbra, pero he elegido este azulejo del Palacio Nacional de Sintra por su diseño sencillo y la armonía de los dos colores predominantes, lo que aumenta el efecto de contraste. Como vemos, esta complementariedad se traduce en una complementariedad numérica en los canales RGB (la mezcla aditiva de ambos colores da blanco).
Si sacamos una foto del azulejo (o cualquier región rectangular que tesele por traslación) y la colocamos como imagen de relleno de cualquier figura plana, como un círculo, al mover la figura, la imagen se moverá por el teselado. Así que basta activar el rastro para reproducirlo. Ahora bien, esta táctica, aunque muy vistosa, solo vale para azulejos rectangulares, es poco operativa para cambiar rápidamente los colores y tampoco permite invertir el azulejo, como vamos a hacer.
La construcción permite no solo la traslación del azulejo por todo el plano (usando la espiral de Ulam), con esos u otros colores, sino también su inversión. Para lograrlo sin que GeoGebra se resienta ante la multiplicidad de objetos, en cada paso solo se traslada un azulejo (ya sea una vez invertido o no), de modo que los azulejos que van apareciendo no son nuevos objetos sino el rastro que va dejando un único azulejo (Losada, 2025). También podemos ver el mosaico en perspectiva, usando la vista 3D.
Ahora nos centraremos en las teselaciones regulares. En la geometría euclídea solo existen tres: la triangular, la cuadrada y la hexagonal. Usando la notación {p, q}, donde p es el número de lados del polígono regular y q es el número de polígonos que rodean cada vértice, esas teselaciones se expresan como {3, 6}, {4, 4} y {6, 3}.
Observemos que {3, 6} y {6, 3} son duales, mientras que {4, 4} es autodual. Si q es par (triángulos y cuadrados), la simetría resultante provoca que los lados de cada polígono descansan todos sobre el mismo conjunto de rectas y el número cromático es 2. Si q es impar (hexágonos), se rompe esa simetría, de modo que las líneas que unen los lados ya no son rectas, sino quebradas, y el número cromático es 3.
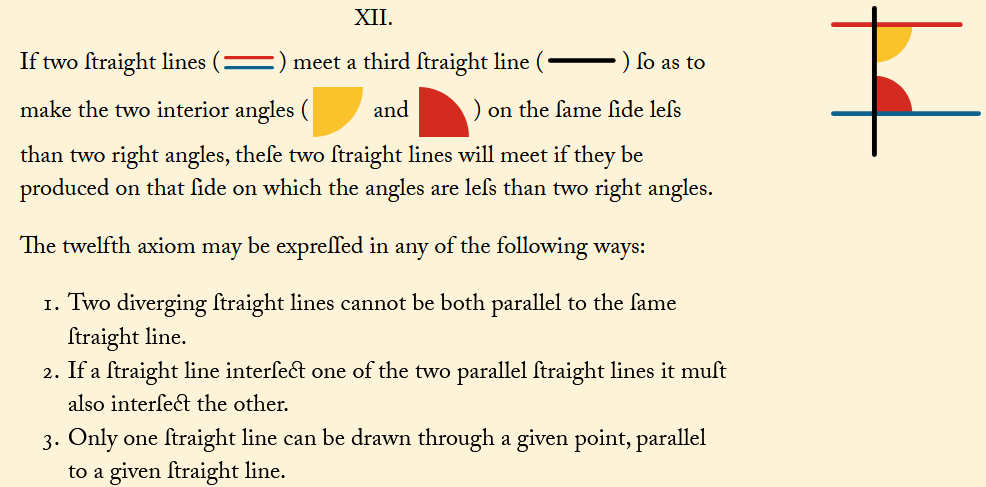
Libro I. Postulado V de los Elementos de Euclides (reordenado en la edición de Oliver Byrne como Axioma XII)
Podemos diferenciar la geometría euclídea de las que no cumplen el quinto postulado de Euclides, la elíptica y la hiperbólica, usando configuraciones {p, q}, es decir, polígonos regulares de p lados donde en cada vértice coinciden q. En particular, el valor de la expresión (p – 2)(q – 2) discrimina cada geometría. Cuando es 4, tenemos tres casos posibles (teselados regulares habituales). Cuando es menor que 4, obtenemos las cinco particiones regulares de la esfera, origen de los cinco sólidos platónicos.
Nota: en esta clasificación suponemos que los polígonos de la teselación regular tienen al menos 3 lados. En la geometría elíptica pueden darse teselaciones con polígonos de 2 lados (¡incluso solo 1!).
Las rectas de la geometría euclídea se convierten en circunferencias máximas en la esfera (como dos de estas circunferencias siempre se cortan, no existen paralelas, por lo que no se cumple el postulado de las paralelas).
Para obtener las cinco particiones de la esfera, convertimos las aristas de los poliedros en arcos de círculos máximos. Usando este mismo procedimiento, podemos convertir cualquier mosaico plano (geometría euclídea) en uno esférico (geometría elíptica). Si se dispone de una impresora 3D, estos mosaicos pueden servir de lámparas personalizadas 🙂.
Para colorear cada polígono esférico recurrimos a las funciones arg() y alt(), con las que se puede transformar fácilmente un polígono (plano) en una superficie esférica, cuyo rastro de color cambiante permitirá cubrir toda la esfera. Pero crear cada polígono esférico consume muchos recursos, así que, para nuestro mosaico, optamos por crear pequeños arcos de círculos, con el rastro activado, en vez de superficies (Losada, 2025).
¿Qué sucede cuando (p – 2)(q – 2) es mayor que 4? Con GeoGebra, podemos averiguarlo. Al igual que en la geometría elíptica el tamaño de cada polígono regular queda determinado por la esfera, ahora quedará determinado por el círculo unidad (recordemos que en la geometría euclídea el polígono es escalable, puede tener cualquier tamaño).
En el disco de Poincaré, las rectas de la geometría euclídea se convierten en arcos de circunferencias ortogonales a la circunferencia unidad (de modo que por un punto exterior a uno de ellos se puede trazar más de uno que no lo corte, por lo que no se cumple el postulado de las paralelas).
La construcción no hace uso de ninguna herramienta de geometría hiperbólica, solo usa repetidamente el comando de inversión en determinadas circunferencias. Igual que antes, gracias al rastro dejado por cada celda, solo necesitamos actualizar una celda (reflejándola en la siguiente), por lo que GeoGebra conserva en todo momento su capacidad de cálculo y ejecución. Para ello basta adaptar a la geometría hiperbólica la espiral de Ulam usada en la construcción euclídea, consiguiendo discos de Poincaré (Losada, 2025) ideales como posavasos 🙂.
Así, podemos ver las cadenas de Steiner que se generan, crear nuestra propio teselado con el azulejo que queramos, generar el disco con el grupo triangular que Coxeter le envió a su amigo Escher, la respuesta de este en forma de grabado (Circle Limit I), la autodualidad, y, en general, generar cualquier teselado hiperbólico regular {p, q}. El número cromático (nc) no depende de la geometría (pues el grafo dual es un concepto topológico), solo de los valores {p, q}. Cuando q es par, nc es 2. Cuando q es 3 y p es impar, se forma una rueda de un número par de vértices (Wp+1), por lo que nc es 4. En los demás casos, nc es 3.
Seguramente, estas son las primeras teselaciones "completas" en el disco de Poincaré realizadas con GeoGebra y, muy probablemente, este es el primer mosaico hiperbólico realizado con un azulejo de influencia mudéjar encontrado en Portugal 🙂. Ahora bien, para realizar cualquier otro similar basta con cambiar el contenido de las listas que definen el azulejo central, sus reflexiones sucesivas se efectuarán automáticamente.
La construcción del azulejo fundamental suele ser una actividad muy instructiva. En este ejemplo, se muestra cómo crear, partiendo de un tetraedro, un azulejo que tesela el plano por traslación. Cortamos el tetraedro siguiendo un camino hamiltoniano, es decir, pasando la tijera o el cúter una sola vez por sus cuatro vértices.
Después, desarrollamos el tetraedro. Está demostrado que la figura resultante siempre tesela el plano (Akiyama & Matsunaga, 2015).
Podemos usar listas vacías como almacenes para guardar los datos. En este caso, usaremos la lista "reg" que almacena los datos de las posiciones de un punto móvil para sustituir su rastro por la poligonal que une todas esas posiciones. Cada vez que el punto P cambia de posición, se ejecuta la instrucción Valor(reg, Añade(P, reg)).
La ventaja de este método es que por una parte mejora la visualización del recorrido realizado, y por otra nos permite estimar su longitud.
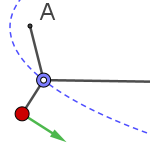
Podemos asignar un guion a un deslizador animado, de modo que cada vez que se actualice su valor ejecute las instrucciones de GeoGebra en él contenidas. Este procedimiento, junto con el rastro activado, nos permite visualizar el recorrido de los puntos que siguen esas instrucciones.
En este ejemplo, el guion compara la suma de distancias a cuatro puntos fijos con la que sería en el caso de que cada uno de los dos puntos se moviera en determinada dirección. Si la suma resultante es menor que la de partida, los puntos se moverán, hasta alcanzar la suma mínima (puntos de Steiner).
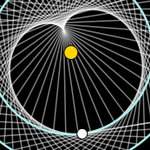
El punto naranja representa el Sol, el azul, la Tierra, y el blanco, Venus.
Cada 8 años, Venus da casi exactamente 13 vueltas alrededor del Sol. En ese
tiempo, Venus adelanta 5 veces a la Tierra, generando una envolvente que recuerda
a 5 cardioides entrelazadas (sería una
cardioide si el año terrestre durase el
doble que el venusiano).
GeoGebra permite crear el diagrama de Voronoi. Aunque solo traza el diagrama, se pueden colorear las regiones recogiendo posteriormente la información suministrada por el grafo. En esta construcción se pueden observar las diferentes regiones, así como la triangulación de Delaunay y el cierre convexo de hasta 50 sitios.
Ahora bien, hay situaciones en las que el comando Voronoi comete errores. Además, presupone que la distancia que estamos empleando es la distancia euclídea (L2). Gracias al rastro de color, podemos comprobar el diagrama correcto y crear otros basados en otras distancias. En este ejemplo, lo hacemos con la distancia taxi (L1) y la distancia tablero de ajedrez (L∞), ambas de circunferencias cuadradas. Este es el procedimiento:
1. Creamos un deslizador r de 0 a d, con d suficientemente amplio (por ejemplo, la mayor distancia entre los sitios). 2. Creamos las circunferencias con centro en cada sitio y radio r. Asignamos un color distinto a cada una y activamos su rastro. 3. Animamos el deslizador r para que tome valores decrecientes desde d hasta 0.
Así, a medida que cada circunferencia reduce su tamaño, su rastro afectará a cada píxel, que quedará con el color de la última circunferencia que lo alcance. Esta será la que tenga su centro (que es un sitio) más próximo a ese píxel (Losada, 2010).
Hasta el siglo XVIII, la matemática no está preparada para abordar el intrigante problema de determinar el movimiento de una
cuerda tensa al pulsarla, un problema que originará lo que hoy se denomina
Análisis armónico.
Rastro de color dinámico
Hipérbolas cortando los lados de un
triángulo en partes proporcionales (ver Apéndice II)
Podemos aprovechar la combinación de las propiedades Rastro y Color Dinámico para crear un poderoso y versátil artilugio de exploración de las relaciones existentes (y posiblemente ocultas) entre objetos matemáticos.
Estamos acostumbrados a ver e interpretar mapas de calor como los que recogen las variaciones de altitud en topografía y de presión o temperatura en meteorología. En esta sección veremos cómo crear un mapa matemático de calor con GeoGebra y algunas de sus aplicaciones.
Coloquemos un punto libre con el rastro activado y definamos su color dinámico en función de la condición c que deseamos visualizar. Como cada canal RGB requiere un valor entre 0 y 1, no colocamos directamente la condición c como valor de cada canal, sino que en su lugar ingresamos cualquier función h tal que h(c) ∈ [0,1].
La función h puede ser, por ejemplo, h(c) = |cos(𝜋/2 c)|. O bien, h(c) = 1/(1+|c|). Si queremos resaltar más los valores próximos a 1, podemos añadir un coeficiente k mayor que la unidad: h(c) = 1/(1+k|c|). Aquí usaremos la función exponencial h(c) = e-|c|.
Nota: Naturalmente, en el caso de la función exponencial (que será el que usaremos habitualmente), la base e puede ser sustituida por cualquier otra como 2, 3, 10... De cualquier modo, solo cuando c sea 0 el valor del canal será 1, estando tanto más cerca del 1 cuanto menor sea en valor absoluto c.
Podemos sustituir el punto con el rastro activado por un cuadradito. Esto resulta conveniente cuando queremos conservar la visualización de los ejes cartesianos o de una imagen de fondo, pues un punto no permite controlar su opacidad, pero un polígono sí.
Inspirado por António, como respuesta creé el primer escáner de color dinámico, un solo punto que barría sistemáticamente toda la pantalla (Losada, 2009). Solo tardó cuatro horas en completar la tarea 🙂, pero cuando regresé a ver cómo iba, faltó poco para que sufriera el síndrome de Stendhal.
El rastro de color
dinámico es una herramienta poderosa para la investigación. Sin embargo, el
movimiento manual del punto que deja el rastro resulta bastante incómodo, a la
vez que impreciso.
Gracias a la herramienta Deslizador, podemos animar automáticamente ese
punto, de forma que recorra los píxeles de la pantalla. Usando la Hoja
de Cálculo (incorporada a GeoGebra en junio de 2009), podemos obtener la misma imagen
(que puede recordar al
efecto de
anillo de
diamantes en un eclipse total de sol) en pocos segundos, pues a partir del punto
que deja rastro es muy sencillo crear una columna o una matriz de puntos (o de cuadraditos)
que lo acompañen, creando un escáner de color dinámico (Losada, 2010).
Nota importante: si se desea modificar la construcción, es recomendable eliminar temporalmente las celdas de las
columnas B, C... de la segunda fila y siguientes antes de realizar cualquier
modificación que afecte a todas esas celdas, pues GeoGebra podría colgarse ante
tanto cambio masivo. Una vez realizados los cambios deseados en las celdas de la
primera fila, basta arrastrar estas celdas hacia las siguientes filas para
reconstruir la tabla entera.
Explorando lo
desconocido
Descubrí la potencia de este método basado en el rastro de
color dinámico el 8 de marzo de 2009. Pero no fue hasta algunos días después
cuando surgió la oportunidad de aplicarlo a una investigación real. Con
motivo del
Seminario Intergeo/GeoGebra
celebrado en el Centro Internacional de Encuentros Matemáticos, nos reunimos varios colegas en Castro
Urdiales (Cantabria).
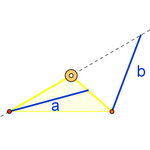
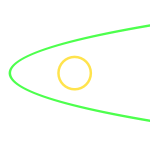
En el transcurso de la cena del 27 de marzo, Tomás Recio
propuso la búsqueda de un lugar geométrico desconocido: dado un triángulo de
vértices fijos A y B, encontrar las posiciones que puede ocupar el tercer
vértice C para que coincidan las longitudes de los bisectores* (interno o
externo) en A y B. Al aplicar el método, esa misma noche pudimos observar cómo
aparecía la figura en forma de lágrima que corresponde al lugar geométrico en el
que un bisector interno "a" tiene la misma longitud que el bisector externo "b".
*Denominamos bisector al segmento de extremos
un vértice y la intersección de cada bisectriz (interna o externa) con el
lado opuesto. Hay, pues, dos bisectores en cada vértice, uno interno y otro
externo (Losada, Recio y Valcarce, 2009).
El lugar encontrado forma
parte de una
curva algebraica de grado 10. (No
es posible distinguir algebraicamente un bisector interno de uno externo sin
recurrir a inecuaciones, por eso este polinomio engloba más casos que el
analizado en el escáner.)
La expresión para canal de color RGB es e-|c|,
donde c varía según el canal, lo que nos permite no solo mostrar (en
blanco) el lugar geométrico buscado, sino también diferenciar por color las
inecuaciones b < a (tonos rojizos) y a < b (tonos azules). Así, para el canal
rojo, c = (a - b) b/a. Para el verde, c = a - b. Para el azul, c = (a - b) a/b.
Pentágono de área dada
Veamos un ejemplo sencillo. Dado un cuadrilátero de área
30, deseamos añadir un nuevo vértice de modo que al intercalarlo entre
los otros cuatro (conservando su orden) el pentágono resultante tenga área 40. ¿Dónde debemos colocar ese nuevo vértice? Podemos tantear con
intersecciones de la cuadrícula, pero así solo lograremos encontrar un punto
válido.
Al pasar el escáner observamos que vale cualquier punto de
un cuadrilátero de lados paralelos al original. Ahora podemos preguntar a
nuestros alumnos: ¿Por
qué? ¿Y cómo se construye ese nuevo cuadrilátero?
Una ventaja del uso de los mapas de calor es que los
alumnos no pueden "hacer trampa" rebuscando la construcción en el archivo, pues
el cuadrilátero que están visualizando no está construido, ni existe ninguna
pista para construirlo.
Distancia al más
lejano, la suma de distancias a los otros dos
Podemos plantear, de este modo, todo tipo de situaciones,
desde las más sencillas como la anterior, hasta las más sofisticadas. Por
ejemplo, en este caso partimos de tres puntos fijos dados y deseamos visualizar
el lugar de los puntos que distan del más lejano la suma de
distancias a los otros dos puntos. El resultado corresponde a los ceros de una curva
algebraica de grado 4.
Tanto este ejemplo como los dos anteriores muestran lugares
que no se pueden obtener con otras herramientas geométricas, ni siquiera con el comando LugarGeométrico.
Naturalmente
Si asignamos un número natural a cada píxel, podemos
visualizar la distribución de colecciones de números naturales. En este ejemplo, he ordenado
los píxeles siguiendo el orden occidental de lectura, es decir, de
izquierda a derecha y de arriba abajo, de modo que el número 1 es el píxel de la
esquina superior izquierda.
Así, en el primer cuarto de millón de números naturales, vemos la diferencia de distribución entre
las sucesivas potencias de 2 (17 números), los números de Fibonacci (26), el número de lados de
los polígonos construibles (166), los números cuadrados (500) y
los números primos (22044). El bajo número de los tres primeros casos nos
recuerda que, en esencia, los tres dependen de una exponencial. En el último
caso, la imagen resultante puede servir de decoración de papel de
regalo 🙂.
Los Elementos, libro I, proposición
47: teorema de Pitágoras
Teorema de Pitágoras
De acuerdo con la leyenda, sobre la puerta de la Academia
de Platón estaba grabado "No entre quien no sepa Geometría" (AΓΕΩΜEΤΡΗΤΟΣ ΜΗΔΕIΣ ΕIΣΊΤΩ).
Podemos ver una réplica de esta frase en la fachada del edificio en el que
estamos.
En la misma fachada, a la izquierda de esa frase, aparece
la conocida figura del "molino" que representa el teorema de Pitágoras y, bajo
ella, una demostración basada en la proporcionalidad de los lados de los
triángulos semejantes (primer teorema de Tales) o en el teorema de la altura.
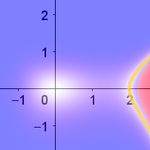
Los mapas de color pueden servir de introducción a
resultados teóricos como este. Tenemos un triángulo de base BΓ y nos
preguntamos dónde debemos colocar el tercer vértice A para que la suma de las
áreas de los cuadrados azules coincida con el área del cuadrado rojo.
Una vez obtenido el mapa, vienen las preguntas: ¿por qué
aparece una circunferencia? ¿qué diámetro tiene? ¿cuánto mide el ángulo que
abarca ese diámetro en cualquier punto de la circunferencia? Observemos que el
mapa representa tanto al teorema de Pitágoras como a su recíproco, es decir, se
cumple la relación entre los cuadrados si y solo si el triángulo es rectángulo,
lo que sucede si y solo si (segundo teorema de Tales y su recíproco) el tercer
vértice está en esa circunferencia.
Nota: En este caso, la información que aporta el mapa es similar a la que
aportan los comandos EcuaciónLugar y Demuestra. Si llamamos
a, b y c a los lados enfrentados respectivamente a A, B y
Γ, EcuaciónLugar(a² ≟ b² + c², A) devuelve la
circunferencia, mientras que si A es un punto de la circunferencia, Demuestra(a²
≟ b² + c²) devuelve "true".
Punto fijo
A veces solo nos interesa conocer la posición de un punto. Aquí vemos, como fondo de pantalla, una vista aérea del centro de Coimbra. Hemos
contraído y distorsionado la imagen, y la hemos superpuesto. Según
el
teorema del punto fijo de Bannach, sea donde sea que posicionemos la segunda
imagen (sin traspasar el perímetro de la primera) existe un único punto en el
que ambas imágenes coinciden.
Ahora bien, lo malo de estos teoremas de existencia (y, en este caso, unicidad)
es que en su demostración no aparece ninguna indicación de dónde se encuentra
ese punto fijo (solo aparece un método de aproximaciones sucesivas). Nuestro escáner nos lo aclara, simplemente sometiendo a los
puntos del escáner a la misma transformación. Así encontramos que, en este caso,
el punto fijo se sitúa (cómo no 🙂) en la estatua de Dom Dinis.
Nota: Empleamos rastros de
cuadraditos en vez de puntos para que el rastro no oculte la imagen.
Bajo el mismo ángulo
La relación buscada puede ser entre ángulos en vez de distancias. Esta
construcción muestra el lugar geométrico de los puntos del plano que forman con
ambos segmentos el mismo ángulo (o, dicho de otra manera, desde los que se ven
ambos segmentos bajo el mismo ángulo). El escáner nos brinda una forma sencilla
de mostrar un ejemplo de lugar geométrico enrevesado y discontinuo.
Además, permite proponer fácilmente problemas particulares con condiciones
añadidas del tipo "¿y si...?". Por ejemplo, qué sucede si los segmentos son
paralelos, o perpendiculares, o los cuatro extremos se sitúan en los vértices de
un cuadrado, etc.
Un canal para cada
condición
Esta construcción es una continuación lógica de la anterior. Dado el triángulo
ABC, aplicamos el escáner con la condición, en cada uno de los canales, de que
cada par de lados del triángulo se vea bajo el mismo ángulo. Los tres lugares
geométricos obtenidos, cada uno con su color correspondiente, solo se cortarán
en aquel punto en que los tres lados se vean con el mismo ángulo (primer centro isogónico,
X(13)). Si todos los ángulos del triángulo son menores que 120º, este punto
caerá en el interior del triángulo, coincidiendo con el punto de Fermat.
Cargas positivas y
negativas
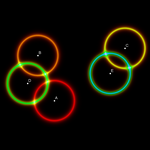
En este ejemplo, tenemos una distribución cualquiera de tres cargas eléctricas positivas
(puntos azules) y otras tres negativas (puntos rojos). Si ahora introducimos una
nueva carga, ¿dónde se producirá el equilibrio? Es decir, ¿en que
posiciones será nula la resultante (suma vectorial) de las seis fuerzas
(atractivas y repulsivas) de la nueva carga hacia las seis cargas existentes?
El escáner nos muestra, en blanco, las posiciones de equilibrio. Pero además,
nos indica que las zonas blancas más amplias son mejores opciones, puesto que
señalan más puntos donde el conjunto no se desequilibra demasiado, son zonas más
"estables".
Nota: la imagen resultante corresponde a la introducción de una nueva carga
negativa. Si fuese positiva, se obtendría la misma imagen solo que cambiando
los azules por rojos y viceversa. Las zonas blancas de equilibrio permanecen,
por tanto, invariables.
Puntos escamoteados
A diferencia de los métodos para representar curvas como los que usa GeoGebra,
el escáner no utiliza ningún algoritmo, por lo que no existe el riesgo de que
aparezcan "excepciones". Aquí vemos que algunos puntos de algunas curvas pueden no
hacerse visibles mediante el método de trazado habitual. El escáner puede
servir para volver a hacerlos visibles.
En el primer ejemplo, el origen de
coordenadas no aparece como punto de la curva y³ - x³ + 4y² + 2x² = 0 en
su representación gráfica habitual.
En el segundo ejemplo, es toda una rama de la curva x⁶ + 3x⁴y - 4y³ = 0 la que
no se visualiza. En el tercer ejemplo, es toda la curva x⁶ - 2x³y + y² = 0
la que permanece oculta. En los puntos escamoteados en todos estos ejemplos, la curva no cambia de signo, se anula sin que esto signifique un
cambio de signo. Esto "despista" al algoritmo de trazado de curvas
implícitas implementado en GeoGebra y otros programas de
cálculo simbólico.
Nota: Algebraicamente, el primer polinomio, cuando y = 0, se puede factorizar
como (-x + 2) x². El segundo polinomio se puede
factorizar como (x² - y) (x² + 2y)². El
tercer polinomio se puede factorizar como (x³ - y)².
Concurrencia de rectas
Veamos otro ejemplo geométrico. Los escáneres en los que cada punto forma parte
de una construcción geométrica suelen ser más lentos que los que comparan
expresiones algebraicas, pues cada fila de la Hoja de Cálculo ha de reproducir
esa construcción geométrica.
En este ejemplo vemos cómo podemos visualizar relaciones como la concurrencia de
varias rectas (o similares, como la alineación de varios puntos). En particular,
nos interesa averiguar cuándo cuatro rectas de Euler concurren en el mismo
punto.
Para ello, partimos de un triángulo ABC, que consideraremos fijo, y añadimos un
cuarto punto libre D. Creamos las rectas de Euler de los triángulos ABD, ACD y BCD,
y sus puntos de intersección con la recta de Euler de ABC. Las rectas
serán concurrentes cuando la distancia entre esos puntos sea nula. Sabemos que
uno de los puntos que buscamos es el incentro, pues las rectas de Euler de los
cuatro triángulos concurren, en ese caso, en el
punto de
Schiffler. Pero, ¿dónde están el resto de los puntos, si es que hay más?
Toda esta información señala a la circunferencia
circunscrita al triángulo ABC y a la
cúbica de Neuberg como el lugar geométrico
al que debe pertenecer el cuarto vértice D para que concurran las rectas de
Euler del cuadrilátero ABCD. Podemos así concluir que, para cumplir esa
condición, el cuadrilátero ABCD debe ser cíclico o bien uno de sus vértices debe
pertenecer a la cúbica de Neuberg determinada por el triángulo formado por los
otros tres.
Descubrimiento de lugares difícilmente algebrizables
En muchas ocasiones, la gráfica del lugar que aparece al pasar el escáner es
difícil de algebrizar con exactitud. Pero incluso si lo que perseguimos es la
expresión algebraica de un lugar geométrico, la visualización que nos ofrece el
escáner facilita en gran medida su búsqueda. La forma de la curva o trazos
visualizados ayudarán a comprender la naturaleza del lugar y el hallazgo de algunos puntos
notables o singulares.
En este ejemplo, el paso del escáner encuentra la bisectriz
entre dos curvas, es decir, el lugar geométrico de los puntos el plano que
equidistan de ambas curvas (Adamou, 2013). El resultado nos permite
calcular dos arcos de elipse que se aproximan mucho al lugar buscado, lo
que puede ser suficiente en numerosas aplicaciones (arquitectura, robótica,
etc.)
Ecuación logística
En este ejemplo, usamos los canales HSL (ver
Apéndice II) para variar el color del
diagrama de
bifurcación de la
ecuación logística xn+1 = r xn (1 - xn) a
medida que aumenta el valor del coeficiente r desde 2.9 hasta 4 (con x0
entre 0 y 1, por ejemplo 0.4). El estudio de esta ecuación
fue uno de los detonadores del nacimiento de la
Teoría
del caos.
Imágenes secuenciales e
imagen de fondo
Como GeoGebra permite exportar e importar imágenes, podemos usar las gráficas
obtenidas para colocarlas de fondo de pantalla y realizar exploraciones sobre
ellas.
Podemos exportar la vista gráfica para diferentes iteraciones y después
visualizarlas secuencialmente. De este modo, se puede
apreciar cómo se va formando el fractal.
También podemos observar cómo las series de potencias forman, para
cada número complejo, polígonos, espirales y otras formas geométricas.
Otros fractales
El conjunto de Mandelbrot no es el único fractal que podemos
escanear. Vale cualquiera que se obtenga por sucesivas iteraciones en cada
punto (definido como número complejo), como los conjuntos de Julia. Por ejemplo,
podemos generar un
fractal de Newton
generalizado. (Ver su creación en el Apéndice II.)
Proyección de un amasijo de tenedores,
cuchillos y cucharas. Lunch With a Helmet On (Almuerzo con casco),
Shigeo Fukuda (1987).
Funciones complejas de
variable real
La fórmula de Euler establece la relación fundamental entre las funciones
trigonométricas y la función exponencial compleja. Richard Feynman se refirió a esta igualdad como la más notable
fórmula matemática.
exi = cos(x) + i sen(x)
Funciones complejas de
variable compleja: Fase sobre módulo
(dominio coloreado)
También podemos visualizar, de modo análogo, el módulo como superficie y la
fase
como color. A esta representación se le conoce como "dominio coloreado" (Breda,
Trocado & Santos, 2013).
Para resaltar los cambios de color, se
sustituyen los
canales RGB por HSL. También podemos añadir líneas de nivel.
La idea consiste en asignar un patrón de color a un rectángulo del plano
complejo (patrón que podemos observar seleccionando la vista XZ de f(z) = z) y
observar su transformación (rotación, reflexión, etc.) al elegir otra función
compleja, como la del apartado anterior.
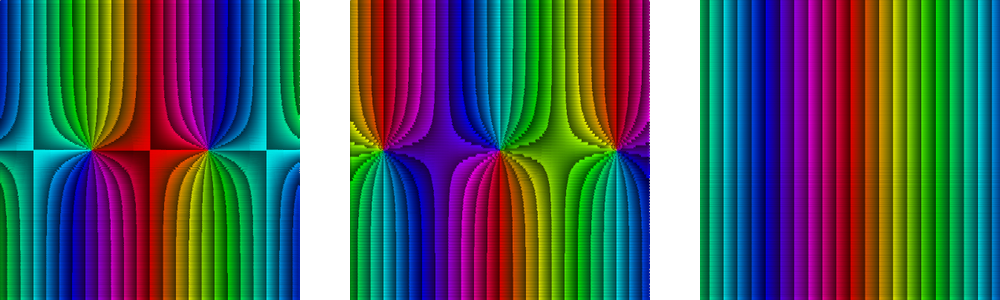
En el caso de la función f(z) = ezi, podemos observar
que la fase depende únicamente de la parte real de z.
De izquierda a derecha, las imágenes de los
dominios coloreados de cos(z), i sen(z) y
ezi.
Rastro de tiempo
Registro del tiempo
Del mismo modo que hemos visto que podemos
crear una lista de posiciones, gracias al comando TomaTiempo() podemos crear una lista que almacene los
datos del tiempo real transcurrido. Esto nos permite simular experimentos cinemáticos
sin usar ni fórmulas ni trayectorias predefinidas
(Losada, 2024). Veamos algunos ejemplos (un par de ejemplos más, como la
Tautócrona o la Braquistócrona, pueden verse en el Apéndice III).
Caída por un plano
El movimiento de caída libre se produce demasiado
rápido para que en tiempos de Galileo se pudiese observar con precisión.
Gracias al
plano inclinado, que ralentiza la caída, Galileo pudo realizar
mediciones con suficiente exactitud para llegar a la conclusión de que la
velocidad de caída varía uniformemente en cada unidad de tiempo.
Péndulo simple
En este ejemplo el rastro es triple: el rastro del
tiempo nos permite medir el período del péndulo, mientras que mediante el
rastro de color dinámico podemos visualizar los cambios en la velocidad
(máxima para el rojo) al mismo tiempo que un punto traza la gráfica
de la elongación angular en función del tiempo. Y todo ello sin hacer uso de
la trigonometría ni de ecuaciones
diferenciales.
Usamos HSL para resaltar los
cambios de color. El registro del tiempo nos permite
comprobar que, en general, el
péndulo simple no sigue un Movimiento Armónico
Simple (MAS). Solo se aproxima mucho a él cuando la amplitud angular es pequeña
(menor de 10º, aproximadamente), pero incluso para una amplitud de 45º las
gráficas son similares. Aumentando la amplitud, podemos comprobar que, en
realidad, la gráfica no es una sinusoidal.
A partir de 130º, el cálculo aproximado del período teórico
conlleva trabajar con números demasiado elevados, por lo que GeoGebra no
lo puede calcular con suficiente precisión, mientras que el período de la
animación sigue ajustándose bastante bien al modelo ideal. Para amplitudes
mayores de 175º, el período seguiría aumentando y tiende a infinito al
acercarse la amplitud a 180º.
Péndulo doble
Si colocamos un péndulo en el extremo móvil de otro,
obtenemos un
péndulo doble. Aunque cada uno de ellos se sigue
rigiendo por el período estable de un movimiento ordenado, su movimiento
combinado resulta caótico.
Podemos aprovechar la poligonal generada por el
rastro para estimar la longitud recorrida por el segundo péndulo. Además
hemos usado los canales HSL para añadir un segmento cuyo rastro es más
claro cuanto mayor sea la velocidad.
Efecto dominó
Podemos visualizar el efecto dominó encadenando una
serie de péndulos. También podemos comprobar que la velocidad de
propagación del movimiento no es proporcional a la gravedad. Aunque la
gravedad en la superficie terrestre es unas 6 veces mayor que en la
superficie lunar, la velocidad de propagación en la Tierra es solo del
orden del doble, o menos, que en la Luna (cuanto menor sea la distancia entre las
fichas, menos diferencia habrá).
El péndulo de Foucault
en la Universidad de Coimbra
Hace exactamente 10 años aparecía
la noticia de la inauguración (el día 25 de octubre) del
péndulo de Foucault
en la Universidad de Coimbra.
Si aplicamos al tiempo una escala 1:3600, podemos visualizar una vuelta
completa de la Tierra en solo 24 segundos (pero solo colocando el péndulo
en uno de los polos). Esta escala de tiempo nos
permite observar el comportamiento del péndulo de Foucault en cualquier
punto terrestre. Si lo colocamos en el hemisferio norte, la rotación
aparente del plano del péndulo se realizará de modo retrógrado (sentido
horario), mientras que el hemisferio sur se realizará de modo directo
(sentido antihorario).
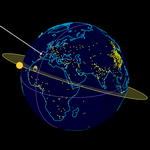
Geometría elíptica. Posición y tiempo
El paso del tiempo también deja su rastro en otros
astros, además de la Tierra. El conocimiento de la posición de estos
astros, como el Sol, la Luna y las estrellas, puede indicarnos en qué
punto de la Tierra nos encontramos en un instante dado.
Podemos elegir la zona horaria (dentro de tres días Portugal pasa
de UTC+1 a ser UTC+0), la fecha y hora (o pulsar "Ahora") o un solsticio o
equinoccio. También podemos mover hasta 3 puntos (A, B y C) sobre la
superficie esférica (aparecerá un rótulo con la ciudad más cercana, o bien
Coimbra o bien otra que sea capital o tenga más de un millón de
habitantes; pulsando sobre ese texto el punto irá a esa posición).
Rastro 2D
↔ 3D
Ptolomeo denominaba Cosmografía a la combinación de
Matemáticas, Geografía y Astronomía que ayudaba a la representación del mundo.
Su estudio ha sido esencial desde los principios de la Edad Moderna, cuando los
marinos españoles y portugueses necesitaban esos conocimientos, entre otros,
para cruzar con éxito el océano Atlántico.
Gracias a los guiones, podemos transmitir cualquier acción
en un objeto a otro... y viceversa. En este ejemplo, se transmite la posición de
un punto en el globo terrestre (superficie esférica en la vista 3D) a su
correspondiente posición en la proyección cilíndrica conocida como
mapa de Mercator (vista 2D). Y recíprocamente. Así, cualquier rastro del primer punto se
convierte en el rastro correspondiente del segundo, y viceversa.
En esta construcción se puede observar la diferencia entre
las curvas ortodrómica (mínimo recorrido) y loxodrómica (rumbo constante).
Recordemos que el descubridor de esta curva fue
Pedro Nunes, genial matemático portugués del siglo XVI
cuyos últimos 34 años los vivió aquí, en Coimbra (donde hoy un centro
tecnológico y una calle comparten su nombre). Nunes se dio cuenta de que esa
curva no era, en general, una circunferencia, sino una hélice esférica.
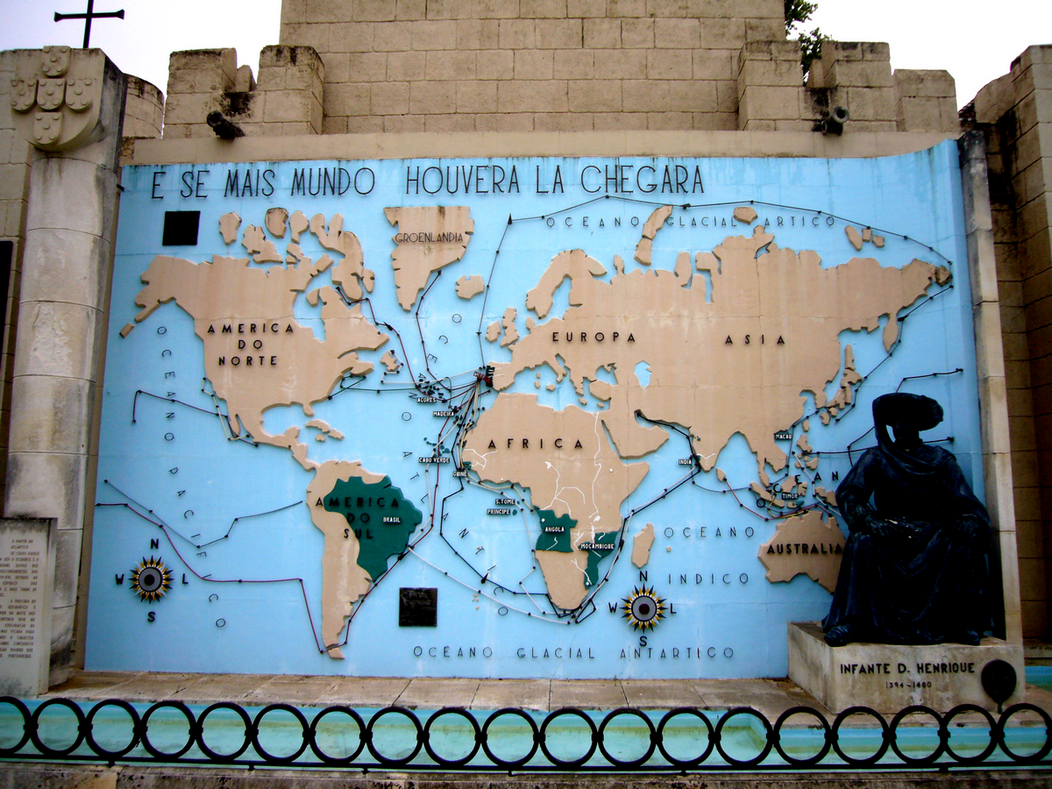
¡Cómo le habría gustado a Nunes y a los famosos
exploradores y descubridores haber podido jugar con una construcción como esta! (La
siguiente imagen se encuentra en el
parque Portugal dos Pequenitos, aquí en Coímbra, uno de los primeros parques de
miniaturas del mundo; generalmente, un niño reconoce
un mapa mundi antes de saber multiplicar. Y, si hubiera más Mundo, habría llegado hasta allí, Luís de Camões,
Los lusiadas, VII-14, último verso.)
Conclusión
Gracias a la observación de todos estos rastros, GeoGebra nos ayuda a explorar
las relaciones Matemáticas en el plano, en el espacio y hasta en el tiempo.
Agradecimientos
Ante todo, deseo expresar mi agradecimiento particular al profesor José Manuel Dos
Santos y, en general, al comité organizador de este congreso, por invitarme
a participar en él.
Como ya es habitual, también quiero agradecer al profesor Tomás Recio su
interés, conocimiento y ayuda, durante muchos años, en diferentes
aspectos de los temas aquí tratados.
Agradezco también a a
Mariló Fernández Mira las fotos de los arcos y
rosetones del claustro de la Sé Velha de Coimbra.
Finalmente, debo recordar al profesor António Ribeiro
por su aportación en el
antiguo foro de GeoGebra para la mejora de la estética del método de rastro de color.
El autor
En mis 40 años de docencia como profesor de Enseñanza Secundaria, en la
búsqueda de incentivar el interés del alumnado, he investigado la
conexión de las Matemáticas con otras áreas, cercanas o implícitas, tan diversas como la
Resolución de problemas,
los
Juegos,
la Percepción
y la Música.
La llegada de la Geometría Dinámica supuso nuevas y grandes oportunidades
para atraer a los estudiantes y promover la creación de sus propias
construcciones.
Mi relación con GeoGebra se remonta a 2005, año en que conocí este
programa creado por Markus Hohenwarter,
aunque ya había trabajado con otros programas de geometría dinámica. Dos
años después, en 2007, el profesor
Tomás Recio me convoca al
Centro Internacional de Encuentros Matemáticos (CIEM,
Cantabria) que reunió, entre otros, a varios profesores de secundaria
españoles pioneros en el uso
didáctico de la geometría dinámica. En esa reunión defendí la eficiencia
de GeoGebra (Losada, 2007) frente a otros programas como Cabri.
Una consecuencia de ese
encuentro fue la formación del grupo
G⁴D,
constituido por J.M. Arranz, J.A. Mora, M. Sada
y el que esto escribe.
Dos años más tarde, desde el Ministerio de Educación de España,
Antonio Pérez,
entonces director del Instituto de Tecnologías
Educativas (ITE, hoy INTEF),
me encarga la realización de cursos para la formación en GeoGebra del profesorado de Educación Primaria y Secundaria, así como la creación de
un conjunto de actividades completas (introducción del tema, construcción
a explorar y cuestionario) para el alumnado, clasificadas por temas y
niveles, que bautizamos como
Proyecto Gauss (al que un cambio político en Asturias interrumpió
abruptamente). Simultáneamente, Tomás pone en
marcha el
primer Instituto GeoGebra en lengua española, el
Instituto GeoGebra de
Cantabria, del cual soy Formador
desde su creación.
Bibliografía
y referencias
Tacquet, A. (1683).
Elementa
geometriae planae ac solidae, quibus accedunt selecta ex archimede
theoremata [Elementos de geometría plana y sólida, a los que se añaden
teoremas seleccionados de Arquímedes.]. Biblioteca Virtual del Patrimonio Bibliográfico.
Byrne, O. (1847).
The first six
books of The Elements of Euclides [Los primeros seis libros de Los
Elementos de Euclides]. William Pickering.
Coxeter, H.S.M. & Greitzer, S.L (1967).
Geometry Revisited [Geometría revisitada]. New Mathematical Library. The Mathematical
Association of America.
Coxeter, H.S.M. (1979).
The non-euclidean symmetry of Escher's picture Circle Limit III
[La
simetría no euclídea del cuadro Círculo Límite III de Escher].
Leonardo, Vol. 12, pp. 19-25 Pergamon Press, Great Britain.
Coxeter, H.S.M. (1997).
The Trigonometry of Hyperbolic Tessellations [La trigonometría
de las teselaciones hiperbólicas]. Canadian Mathematical Bulletin.
Ortega, E., Ortega, I., Ortega, T., Crespo, C. (2005)
La
motivación de la belleza. UNIÓN (Revista Iberoamericana de
Educación Matemática) Nº 2.
Losada, R. (2007).
GeoGebra: la eficiencia de la intuición.
La Gaceta de la RSME, vol.
10.1.
Hart, S. (2007)
Escher and Coxeter - A Mathematical Conversation [Escher
y Coxeter: una conversación matemática]. Gresham College.
Barth, Amanda (2007).
Tessellations: The Link Between Math and Art
[Teselaciones: el vínculo
entre Matemáticas y Arte].
Trinity University. San Antonio.
Losada, R. (2007-2009).
Música y Matemáticas (enlace roto).
G⁴D en Divulgamat. Real Sociedad
Matemática Española.
Libro
de GeoGebra.
Conway J.H., Burgiel H. & Goodman-Strauss C. (2008)
The Symmetries of Things
[Las simetrías de las cosas]. A K Peters. Wellesley. Massachusetts.
Arranz, J.M., Losada, R., Mora, J.A. y Sada, M. (2008).
Arcos con geometría dinámica (GeoGebra) I y II. Matematicalia,
vol. 4, nº 1 y 2, Real Sociedad Matemática Española.
Libro de
GeoGebra.
Arranz, J.M., Losada, R., Mora, J.A. y Sada, M. (2009).
Geometría en rosetones góticos (enlace roto). G⁴D en Divulgamat. Real Sociedad
Matemática Española.
Libro
de GeoGebra.
Losada, R. (2009).
Magic color: Ghost constructions
(enlace roto) [Color mágico:
Construcciones fantasma].
GeoGebra User Forum.
Losada, R., Recio, T. y Valcarce, J.L. (2009).
Sobre el descubrimiento
automático de diversas generalizaciones del Teorema de Steiner-Lehmus. Boletín de la Sociedad
"Puig Adam" de profesores de matemáticas, nº 82, pp. 53-76. Universidad
Complutense de Madrid. Versión inglesa:
On the automatic discovery of Steiner-Lehmus generalizations (2010, J. Richter-Gebert y P. Schreck, editores, München, pp. 171–174).
Losada, R. (2009).
GeoGebra en
la Enseñanza de las Matemáticas. Ministerio de Educación y Formación
Profesional. CD-ROM. ISBN: 978-84-369-4794-6.
Losada, R. y Álvarez, J.L. (2010).
GeoGebra en
la Educación
Primaria. Ministerio de Educación y Formación Profesional. CD-ROM.
ISBN: 978-84-369-4909-4.
Losada, R.
(2010).
De luz y de color (enlace roto). G⁴D en Divulgamat. Real Sociedad
Matemática Española.
Libro
de GeoGebra.
Losada, R. (2010).
Creador de rosetones. Proyecto Gauss. Instituto Nacional de
Tecnologías Educativas.
Libro de GeoGebra.
Álvarez, J.L. y Losada, R. (2011).
El proyecto
Gauss. Revista SUMA, nº 68, pp. 17-25.
Losada, R., Recio, T. y Valcarce, J.L. (2011).
Equal Bisectors at a Vertex of
a Triangle [Bisectores iguales en un vértice de un triángulo]. Computational Science and Its Applications - ICCSA.
Breda, A., Trocado, A. & Santos, J. (2013).
O GeoGebra para além da segunda dimensão
[GeoGebra más allá de la segunda dimensión]. Indagatio Didactica,
5(1). Universidade de Aveiro.
Adamou, I. (2013).
Curvas y superficies bisectrices y diagrama de Voronoi de una familia
finita de semirrectas paralelas en R³, tesis doctoral.
Losada, R. (2014).
El
color dinámico de GeoGebra. La Gaceta de la Real Sociedad Matemática
Española, vol. 17.3, 525–547.
Libro de GeoGebra.
Requena, A. (2014).
De azulejos y matemáticas. XV Congreso de Enseñanza y Aprendizaje
de las Matemáticas.
Akiyama, J. & Matsunaga, K. (2015)
Treks
into Intuitive Geometry, The World of Polygons and Polyhedra
[Incursiones en la geometría intuitiva, el mundo de los polígonos y
poliedros]. Springer Japan.
Losada, R. (2016).
La Tierra y
el Sol. Libro de GeoGebra. Versión inglesa (incompleta): Earth and
Sun.
Losada, R. y Recio, T. (2021).
Mirando a los
cuadros a través de los ojos de Voronoi. Boletín de la
Sociedad "Puig Adam" de profesores de matemáticas, vol. 112, pp. 32–53.
Libro de GeoGebra.
Losada, R. (2021).
Variable compleja.
Libro de GeoGebra.
Losada, R. (2021).
Julia y Mandelbrot.
Libro de GeoGebra.
Losada, R. (2021).
Redes y grafos: Las comunicaciones y la logística. Exposición
Matemáticas para un
mundo mejor. Red DiMa, Día Internacional de las Matemáticas.
Durán, A.J. (2021).
Matemáticas y belleza. Exposición Matemáticas para un
mundo mejor. Red DiMa, Día Internacional de las Matemáticas.
Pérez, A. (2021).
Fractales, la Geometría del Caos. Exposición
Matemáticas para un
mundo mejor. Red DiMa, Día Internacional de las Matemáticas.
Recio, T., Losada, R., Kovács, Z. y Ueno, C. (2021).
Discovering
Geometric Inequalities: The Concourse of GeoGebra Discovery, Dynamic
Coloring and Maple Tools [Descubriendo desigualdades geométricas: El
concurso de GeoGebra Discovery, coloración dinámica y herramientas de
Maple]. Mathematics 9 (20), 2548.
Losada, R. (2022).
Mapas de c@lor con GeoGebra.
Revista SUMA, nº 102, pp.
43-57.
Libro de GeoGebra.
Losada, R. (2023).
La
geometría del Taxi. Boletín de la Sociedad "Puig Adam" de
profesores de matemáticas, vol. 116,
pp. 10-37. Libro de GeoGebra.
Losada, R. (2023).
GeoGebra Principia.
Conferencia de clausura del I Congreso Internacional de GeoGebra. Libros de GeoGebra:
español,
portugués,
inglés.
Losada, R. (2024).
El dominio del Tiempo
(cinemática intuitiva).
Conferencia en el V Día GeoGebra de España. Libros de GeoGebra:
español,
inglés.
Losada, R. (2025).
La fábrica de teselados.
Libro de GeoGebra.
Losada, R. (2025).
Se hace camino al andar. UNIÓN-Revista Iberoamericana de Educación
Matemática, vol. 21, nº 73.
Losada, R. (2025).
Teselaciones
regulares.
Libro de GeoGebra.
Apéndice I (rastro de
color)
Rastro de rectas: envolventes
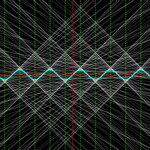
Un ejemplo típico del uso del rastro es la visualización de familias de curvas o
rectas. En este ejemplo, la visualización es doble. A la izquierda, es la
función y = sen(x + k) la que varía el valor k, mientras el punto de tangencia
se mantiene en x = 0. A la derecha, es el punto P de la gráfica de y = sen(x) el
que se desplaza.
Las tangentes en x = 0 de las gráficas de las funciones f(x) = sen(x + k) son
las rectas y = cos(k) x + sen(k). La
envolvente de esta familia de rectas es la
hipérbola equilátera y² - x² = 1, cuyas asíntotas son las rectas y = ±x (k = 0 o
k = 𝜋).
Así, para el punto P, el
rastro de las rectas (k = x(P)), enmarcado por esas asíntotas, formará una
cuadrícula en el plano. También podemos construir directamente la cuadrícula
usando Secuencia(Recta((k 𝜋, 0), (k 𝜋 + 1, cos(k 𝜋))), k, -10, 10).
Apéndice II (rastro dinámico)
Ruido blanco
Podemos usar las coordenadas cartesianas como parte de la
condición de cada canal RGB, lo que permite dividir la pantalla en diferentes
zonas según nuestros intereses.
Si en cada canal RGB colocamos la función random(),
que genera un número aleatorio entre 0 y 1, obtenemos una imagen en el
que el color de cada píxel es independiente del vecino. Esto se denomina
ruido blanco o nieve
electrónica, la conocida imagen (en escala de grises en las televisiones en
blanco y negro) producida por las antiguas televisiones
analógicas cuando no sintonizaban ningún canal.
Ahora bien, si en uno de los canales RGB, por
ejemplo el verde, sustituimos la función random() por una expresión algebraica,
la gráfica correspondiente resaltará sobre el fondo caótico. En este ejemplo, la
expresión para el canal verde es e-|c|, donde c
= |P-A| |P-B| |P-C| - 25, es decir, un
óvalo de Cassini generalizado a tres puntos A, B y C.
HSL
Aunque normalmente no es preciso, si necesitamos
diferenciar con colores más de tres objetos, podemos sustituir los canales RGB
por HSL (Matiz, Saturación, Luminosidad). El modo de gestionarlo es algo más
complicado. En este ejemplo hemos diferenciado las circunferencias de radio r y
centros A, B, C, D y E con estas expresiones:
Matiz: 0.1exp(-5||P-B|-r|)
+ 0.2exp(-5||P-C|-r|)
+ 0.4exp(-5||P-D|-r|) + 0.5exp(-5||P-E|-r|)
Saturación: 1
Luminosidad: 0.5 (exp(-5||P-A|-r|)
+ exp(-5||P-B|-r|)
+ exp(-5||P-C|-r|)
+ exp(-5||P-D|-r|)
+ exp(-5||P-E|-r|))
Cortes proporcionales
Sustituir en los canales de color la función exponencial por otras
expresiones puede generar imágenes inesperadas. En este ejemplo, la hemos
sustituido por una fracción que no siempre toma un valor finito (puntos en
negro).
Misma área y
circunferencia inscrita En este
caso, vemos un triángulo de área 30 u2 y su círculo inscrito. Dos
vértices están en una horizontal (y = -2). Queremos averiguar dónde debe
estar el tercer vértice para que se conserve tanto el círculo inscrito como
el área del triángulo (siempre con base en la recta y = -2, pues consideramos
equivalentes los triángulos congruentes). Nota:
algebraicamente, vemos los puntos (x - y, x
y + 1) 2/(x y - 1) donde (x,
y) es un punto de la curva 2 x² y + 2 x y² - 15 x y + 15 = 0.
Fractal de Newton
generalizado
Podemos generar un
fractal de Newton
generalizado usando la iteración:
zn+1 = zn + a p(z)/p'(z)
Hemos elegido el polinomio complejo p(z)
= (z² + 9)(z - 4) y el número a = 1 + i. Las raíces
del polinomio (puntos atractores) son los puntos rojo, verde y azul. Cada
punto del fractal está coloreado según la distancia (después de
varias
iteraciones) a las raíces, por lo que adquirirá la misma tonalidad que el
de la raíz a la que converge.
Apéndice III (rastro de tiempo)
Estas animaciones simulan el movimiento en tiempo real, despreciando el rozamiento. No hacen uso de fórmulas
(ni trigonometría ni ecuaciones ni cálculo diferencial), solo realizan las
variaciones necesarias en los vectores que dirigen el movimiento.
Tirolina
La carga de una tirolina ideal (es decir, sin
rozamiento) se comporta de modo similar al del péndulo doble. La diferencia
estriba en que ahora la polea (el primer péndulo) no traza un arco de circunferencia, sino
un arco de catenaria. Al colgar una carga, la polea divide el cable en dos
arcos de catenarias diferentes. Si el peso de la carga es grande,
podemos estimar que esos arcos son prácticamente rectos (aunque
físicamente nunca lo serán exactamente), con lo que la
polea recorrerá un arco de elipse, pues su recorrido está determinado por la longitud del
cable, que es la suma de las distancias de la polea a los extremos A y B.
Como la elipse es una curva mucho más simple que la catenaria, elegimos
esta opción.
Aprovechamos el guion del deslizador "anima" para
registrar la máxima velocidad alcanzada. Así, podemos
observar que la carga (punto rojo) puede llegar a moverse más rápido que
la polea de enganche al cable (punto azul). En la realidad, la carga suele
estar muy cerca de la polea, lo que minimiza, junto con el rozamiento, los
vaivenes producidos por la carga.
Tautócrona ("tiempo
igual")
La cicloide es la única curva que tiene la propiedad de ser una curva
tautócrona , es decir, el tiempo que le lleva a una masa que se desliza sin
rozamiento en gravedad uniforme hasta su punto más bajo es independiente de
su punto de partida. Huygens descubrió que ese tiempo es 𝜋/2 veces el
tiempo de caída libre desde la altura del diámetro del círculo que genera la
cicloide. Es decir, el período de oscilación de los tres puntos es siempre
el mismo.
Braquistócrona ("tiempo
mínimo")
La cicloide es la curva de descenso más veloz para ir desde H hasta P. Hemos
añadido la circunferencia que pasa por H, S y P, pues Galileo creía que la
braquistócrona debería ser esa circunferencia (línea verde), pero se
equivocó (aunque no por mucho) como puedes comprobar en la construcción. En
realidad, el punto verde realiza un movimiento pendular, cuyo período de
oscilación es algo mayor que el de la cicloide. Lo que resulta muy evidente
es que la línea recta está muy lejos de ser la mejor opción (aunque mejora
cuanto mayor sea su pendiente, es decir, cuanto más próximo se encuentre P
de H).
|
|