|
|
► 6. Propuestas sencillas de construcción
► 6.4 Problemas
Mathema
La raíz de la palabra Matemáticas es griega y significa "conocimiento, enseñanza", es decir, lo que se aprende y enseña. Ahora bien, ¿con qué finalidad? Lo que se aprende y enseña... ¿para qué?
La respuesta es simple: lo que se aprende y enseña para poder superar dificultades, esto es, resolver problemas.
Los problemas son el origen y fin de las Matemáticas desde hace más de cuatro mil años. Antiguos problemas de reparto, parcelas, contabilidad, arquitectura y astronomía sentaron las bases de la aritmética, la proporcionalidad, la geometría euclidiana, los sistemas de numeración, los métodos de medición...
Como los métodos matemáticos tienden a la generalización como vía de resolución de problemas concretos, rápidamente la propia matemática crea un enorme número de problemas generales ("teoremas") de las propias Matemáticas, resueltos o todavía sin resolver.
Los actuales problemas de la física cuántica, de la bioingeniería genética, de los sistemas caóticos, de las comunicaciones digitales... requieren nuevos métodos para resolverlos, nuevas Matemáticas, que de esta forma se mantienen vivas como nunca, abriendo nuevas regiones del conocimiento y alcanzando nuevos resultados a un ritmo muy superior a cualquier momento anterior.
En definitiva, los problemas son el corazón mismo de las Matemáticas: "hacer matemáticas" es esencialmente "resolver problemas".
Tecnología GeoGebra
De la misma forma que un mecánico agradece una buena caja de herramientas como ayuda para resolver una gran variedad de problemas, las herramientas de GeoGebra nos permiten abordar más fácilmente muchos tipos de problemas, e incluso atacar algunos tipos que sin su ayuda serían, en un determinado nivel de enseñanza, prácticamente inviables.
Detallaremos a continuación un ejemplo.
Un problema difícil (o no tanto)
Veamos ahora el siguiente enunciado:
Las diagonales de algunos trapecios son mutuamente perpendiculares. A esos trapecios especiales los llamaremos "trapecios ortodiagonales". Dados dos puntos fijos A y B, ¿dónde se encuentran todos los puntos de corte de las diagonales de los trapecios ortodiagonales de base AB?
A primera vista, el problema parece al menos del nivel de bachillerato. Para empezar, hay un tipo de dificultad en la misma comprensión del enunciado. Se usan términos desconocidos que "hay que digerir". Hará falta ir desgranando frase a frase ese enunciado, pero veremos que con la ayuda de GeoGebra el proceso se podrá realizar con toda naturalidad.
Las diagonales de algunos trapecios son mutuamente perpendiculares.
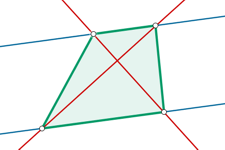
¿Es cierto? Si realizamos algunos ensayos con GeoGebra vemos rápidamente que podemos construir de diversas formas muchos de esos trapecios. Seguramente nos daremos cuenta que si trazamos cualquier par de rectas paralelas y otro par cualquiera de rectas perpendiculares, los cuatro puntos de corte de esos dos pares de rectas son los vértices de esos trapecios.
A esos trapecios especiales los llamaremos "trapecios ortodiagonales".
Bien, eso no añade información, solo es una forma de denominar, para abreviar, a los trapecios cuyas diagonales se cortan perpendicularmente. Sigamos.
Dados dos puntos fijos A y B, ¿dónde se encuentran todos los puntos de corte de las diagonales de los trapecios ortodiagonales de base AB?
Ahora lo único que tenemos que conseguir hacer es construir esos trapecios a partir de la base AB. Tal vez los pasos más naturales para lograrlo sean los siguientes:
- Puntos A y B, los fijamos y trazamos el segmento AB.
- Recta paralela a AB por un punto cualquiera C.
Con eso ya tenemos el par de rectas paralelas. Ahora construiremos las diagonales perpendiculares. Tenemos dos vértices fijos del trapecio, A y B. Colocamos un tercer vértice en cualquier posición de la paralela, con lo que conseguimos una diagonal. El resto es fácil.
- Punto D en la paralela a AB que hemos trazado.
- Recta AD y recta perpendicular a AD por B.
- El punto de corte E de esta última recta con la paralela a AB es el cuarto vértice del trapecio.
Hemos usado GeoGebra para "reconstruir las condiciones del problema". Una vez hecho, la movilidad del punto D nos permitirá resolver el problema en segundos.
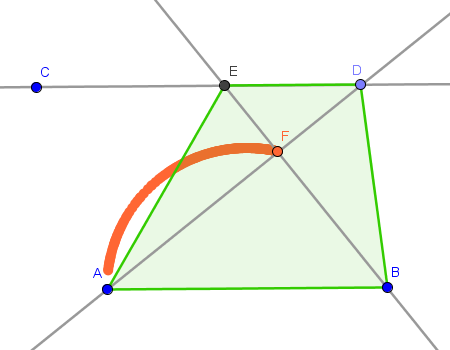
- Sea F el punto de corte de las dos diagonales. Activamos su rastro.
- Al mover D, F describe una circunferencia de diámetro AB y centro el punto medio de AB.
Observemos que la posición de C, es decir, la altura del trapecio, no importa. El trapecio puede tener una altura de mil kilómetros que dará igual: el punto en que se cortarán las dos diagonales estará siempre en esa circunferencia.
Ejemplo de construcción
|
Usar la Barra de Navegación para distinguir cada uno de los pasos. Al final, mover D. |
|
Clic en esta imagen abre la construcción de GeoGebra |
Propuesta de trabajo
Resolver con ayuda de GeoGebra el siguiente problema:
Sea una circunferencia de centro A y radio 5. Colocamos en esa circunferencia tres puntos (B, C y D) y formamos el triángulo BCD. El baricentro de ese triángulo es la media de los vértices: (B+C+D)/3. Cuando se mueve cualquiera de los tres vértices B, C o D, el baricentro recorre un arco de circunferencia. ¿Cuánto mide el radio de esa circunferencia?
Herramientas:
Estrategia:
Realizar la construcción paso a paso y, una vez realizada, usar el método descrito en Marcas para marcar 3 puntos por los que pase el baricentro al mover un vértice del triángulo. Esos tres puntos determinan la circunferencia buscada. Calcular su radio usando las herramientas
Centro y
Segmento.
Nota: alternativamente, en este caso, en vez de usar marcas podemos emplear
la herramienta
![]() Lugar, más rápida y cómoda.
Lugar, más rápida y cómoda.
Comentarios
El uso combinado de las herramientas de GeoGebra permite convertir la vista gráfica en un avanzado laboratorio matemático en donde poder realizar todo tipo de ensayos, experimentos y comprobaciones con facilidad y rapidez, con la gran ventaja sobre el instrumental físico de no estar limitados por sus dimensiones, flexibilidad, roturas, manchas, desgaste, reposición, peligro de ingestión, peligro de lesión, etc., además de poder conseguir mayor precisión, calidad estética y dinamismo.
![]() Investigación:
Investigación:
- En la propuesta de trabajo, la circunferencia que recorre el baricentro al mover un vértice siempre divide al lado opuesto en tres partes iguales. ¿Es cierto? ¿Por qué? (Indicación: el baricentro se sitúa en la mediana a 1/3 del lado y 2/3 del vértice.)