El matemático francés Abraham De Moivre (1667-1754) demostró que bajo determinadas condiciones la distribución binomial B(n,p) se puede aproximar mediante la distribución normal N(np, ), donde q=1-p, es decir, mediante una distribución normal que tiene la misma media y la misma desviación típica que la distribución binomial.

Cuanto mayor es el valor de n y más próximo a 0.5 es el valor de p, mejor se adapta la curva de la distribución normal a la gráfica de la distribución binomial.

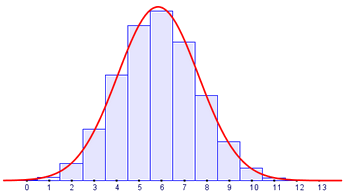
Ajuste de la B(13,0.45) por la N(5.85,1.79)

Para valorar la aproximación de la distribución binomial B(n,p) mediante la distribución normal N(np, ) se suele emplear el siguiente criterio:

• La aproximación es aceptable si n·p y n·q son ambos mayores que 3.

• La aproximación es muy buena si n·p y n·q son ambos mayores que 5.

En la gráfica anterior se puede observar que la curva de la distribución normal N(5.85, 1.79) se adapta muy bien al gráfico de la distribución binomial B(13,0.45). En tal caso se tiene: n=13, p=0.45 y q=0.55, con lo que

n·p=5.85     n·q=7.15

valores que garantizan que la aproximación es muy buena.